In short: I designed a score function for Backgammon that, in a single pass and without dice rolls or search, maps positions into the [0,100] range, is antisymmetric, interpretable, and works at millisecond speed. Below I share its formula, rationale, validation, and how it performs for doubling (cube) decisions.
Y_i, O_i (i=1..24): Number of my and opponent's checkers at point i.b_Y, b_O: Checkers on the bar (me/opponent).y_Y, y_O: Borne-off checkers (me/opponent).f_i: Normalized features, f_i ∈ [-1,1].w_i: Feature weights.D: Raw score (linear + interactions).g(D): D→S transform; tanh(D/σ).S_me, S_op: Final scores (0–100), S_me + S_op = 100.σ=3.0S_me = 50 + 50·g(D), S_op = 100 − S_me → guaranteed antisymmetryIn Backgammon, position evaluation is usually done via search (minimax) or simulation (Monte Carlo). These are accurate but expensive: high latency, high energy consumption, weak for mobile/edge use. My goal was to produce an evaluation function that completes in a single pass, is mathematically robust (antisymmetric, bounded, monotonic), interpretable, and fast.
Raw score and transformation (core definition):
D = Σ w_i · f_i
g(D) = tanh(D / σ), σ = 3.0
S_me = 50 + 50 · g(D)
S_op = 100 − S_me
Antisymmetry guarantee: When you flip the colors and board, all f_i signs change → D → −D → S_me ↔ 100−S_me. Therefore, S_me + S_op = 100 always holds.
f_pip = (PIP_O − PIP_Y) / 375
PIP_Y = Σ i·Y_i + 25·b_Y, PIP_O = Σ (25−i)·O_i + 25·b_OPIP ∈ [0, 375] (all 15 checkers on the bar → 25×15=375; empty board → 0)∈ [−375, +375]; with denominator 375, f_pip ∈ [−1,1] is guaranteed.f_hb = (H_Y − H_O)/6, H_· ∈ {0..6} → difference ∈ [−6,6] → [-1,1]
f_prime = (L_Y − L_O)/6, L_· ∈ {0..6} → [-1,1]
f_anch = (A_Y − A_O)/6, A_· ∈ {0..6} → [-1,1]
f_blot = (W_O − W_Y)/22.5
W_· = Σ ρ(i)·1[·_i = 1], ρ(i) = 1.5 (1..6), 1.0 (7..18), 1.2 (19..24)W_max = 15×1.5 = 22.5∈ [−22.5, +22.5] → [-1,1]f_stack = (S_O − S_Y)/10, S_· = Σ max(·_i−5, 0)
max(15−5, 0) = 10∈ [−10, +10] → [-1,1]f_bar = (b_O − b_Y)/15, b_· ∈ {0..15} → [-1,1]
f_off = (y_Y − y_O)/15, y_· ∈ {0..15} → [-1,1]
f_out = (T_Y − T_O)/12, T_· ∈ {0..12} (points 7–18, 12 in total) → [-1,1]
f_x1 = (H_Y/6)(b_O/15) − (H_O/6)(b_Y/15)
∈ [0,1]; difference ∈ [−1,1]f_x2 = (L_Y·A_O − L_O·A_Y)/36
L_·, A_· ∈ {0..6} → denominator 36 assures [-1,1]Ŷ_i := O_{25−i}, Ô_i := Y_{25−i}, b_Y↔b_O, y_Y↔y_O (see: bras_evaluator.py:306)f_i(Ŷ,Ô) = −f_i(Y,O):
pip: Indices and bar switch signshb/anch/out/prime/stack: Counts swap sign when side changesblot: ρ*(i)=ρ(25−i) — local risk weights flipbar/off: Differences change signx1/x2: Cross terms also swap signD(Ŷ,Ô) = −D(Y,O), S_me(Ŷ,Ô) = 100 − S_me(Y,O)g(x) = tanh(x/σ) → single function; |g|≤1g'(x) = (1/σ)·sech²(x/σ); g'(0) = 1/σ ≈ 0.333 (σ=3)∂S_me/∂D = 50·g'(D)
∂S_me/∂D ≈ 16.67 (high sensitivity; saturates near extremes)|D|≈3 → |g|≈tanh(1)≈0.761 → S≈50±38Increase pip difference R=PIP_O−PIP_Y:
∂S_me/∂R = 50·g'(D)·w_pip/375 > 0 (see: docs/ras_mathematical_foundations.md)Increase my bar b_Y:
∂S_me/∂b_Y = −50·g'(D)·(w_bar/15 + (w_x1·H_O)/(6·15)) < 0 (negative)w_i is “change in D per unit of feature”; score sensitivity is ~50·g'(D)·w_iw_pip=2.2 → 50·(1/3)·2.2/375 ≈ 0.097 score/PIP unit difference> Visualization suggestion: plot D→S curve and g’(D) (sensitivity) together to show high central sensitivity and extreme saturation.
pip: pip difference (across all phases)bar: bar disadvantage (very strong signal)off: bear-off progress (endgame speed)hb: home board strength (hitting/jailing)prime: longest prime (movement restriction)anch: number of anchors in opponent's home (back game security)blot: regionally weighted blot riskstack: penalty for >5 checkers stacked (flexibility loss)out: midboard (7–18) controlx1: hb × bar synergyx2: prime × anchor interaction (dampened via negative weight)Weights and definitions as in the implementation: bras_evaluator.py:55, detailed maths: docs/ras_mathematical_foundationd.md.
Sample 2 from docs, summary:
f_pip ≈ +0.0427, f_blot ≈ −0.0311, f_bar ≈ −0.0667, f_out ≈ −0.0833, f_x1 ≈ −0.0111D ≈ −0.1265 → S_me ≈ 47.893, S_op ≈ 52.107bras_evaluator.py example and test_bras.py:192The S scale (0–100) is ideal for human-readability but is not a direct “win probability.” With real-game or simulation labels (win=1/lose=0), you can calibrate S → p(win) via a simple mapping.
Recommendation: Isotonic regression (monotonic calibration)
Steps (summary):
(S_me, outcome) (outcome ∈ {0,1})S_me values [0,100] → [0,1] (e.g., S' = S_me/100)p̂ = h(S') using isotonic regressionSample code (adapt to your data):
import numpy as np, pandas as pd
from sklearn.isotonic import IsotonicRegression
import matplotlib.pyplot as plt
# df: results from games; S_me (0..100), outcome ∈ {0,1}
df = pd.read_csv('my_games.csv')
S = df['S_me'].values / 100.0
y = df['outcome'].values
iso = IsotonicRegression(out_of_bounds='clip')
p_hat = iso.fit_transform(S, y)
# Reliability curve
bins = np.linspace(0, 1, 11)
bucket = np.digitize(S, bins) - 1
cal = pd.DataFrame({'S': S, 'y': y, 'p': p_hat, 'b': bucket})
grp = cal.groupby('b').agg(S_mean=('S','mean'), y_mean=('y','mean'), p_mean=('p','mean'))
plt.plot(grp['S_mean'], grp['y_mean'], 'o-', label='Empirical')
plt.plot(grp['S_mean'], grp['p_mean'], 'x--', label='Calibrated')
plt.plot([0,1],[0,1],'k:', label='Perfect')
plt.xlabel('S/100'); plt.ylabel('p(win)'); plt.legend(); plt.grid(alpha=.3)
plt.tight_layout(); plt.savefig('ds_analysis/14_calibration_curve.png', dpi=150)
Notes:
S is not equal to p(win) by default; calibration aligns it to real data.σ or w gets updated, recalibrate for best accuracy.Doubling decisions are by nature thresholded. Using this function’s smooth mapping from D to S, here’s a practical guide for money game:
D ≳ 0.5 → S_me ≈ 50 + 50·tanh(0.5/3) ≈ 54–55D ≈ 1.0–1.5 → S_me ≈ 65–70 (position & volatility dependent)D ≳ 2.0–2.5 → S_me ≈ 80+ (opponent passing starts to make sense)Notes:
hb/prime/anch combos affect volatility.S_op = 100 − S_me.ds_analysis_doubling2/dataset.csv.Optional visuals:
ds_analysis_doubling2/01_score_distributions.png: Distribution contextds_analysis_doubling2/07_statistical_tests.png: Statistical consistencyds_analysis_doubling2/08_feature_importance.png: Feature effectsThis section covers the minimal building blocks and sample code for engine integration.
Idea: Score all child positions from legal moves using compute_score, then search best-first.
from tavla_evaluator import TavlaEvaluator
def order_moves(current_position, legal_moves, apply_move_fn, top_k=None):
e = TavlaEvaluator()
scored = []
for m in legal_moves:
child = apply_move_fn(current_position, m) # update position
S_me, _ = e.compute_score(child)
scored.append((m, S_me))
scored.sort(key=lambda t: t[1], reverse=True)
return scored if top_k is None else scored[:top_k]
Note: In expensive search/simulation, this order accelerates pruning (best branches expand first).
[Position] → compute D, S_me
|-- S_me ≥ S_drop → Double → Opponent: Pass (profit ↑)
|-- S_live_low ≤ S_me < S_drop → Double suggested (check position/volatility)
|-- S_me < S_live_low → No double (play on)
Suggested initial thresholds (money game):
S_live_low ≈ 62–65, S_drop ≈ 80Warning: Thresholds depend on game/target; recalibrate with your data. For match play, score/equity needs adjustment.
bras_evaluator.py:47compute_raw_score → bras_evaluator.py:254g_transform → bras_evaluator.py:257 (σ=3)compute_score → bras_evaluator.py:267flip_position → bras_evaluator.py:306Sample positions (match docs): bras_evaluator.py:327, bras_evaluator.py:349
All tests in test_bras.py; auto-generator covers boundaries, monotonicity, and edge cases.
S_me + S_op = 100, after flip S_me' = S_op; max error ~1e−14 (test_bras.py:139)S=50.000; contact example D≈−0.1265, S≈47.893 (tolerance < 1e−2) (test_bras.py:192)f_i ∈ [-1,1] (no violations) (test_bras.py:240)S ∈ [0,100] (no violations) (test_bras.py:274)test_bras.py:303)test_bras.py:402)Output and performance:
Produced EDA, correlations, importance (|w|·std), transformation behavior and sensitivity analyses.
Highlights:
IMG/bras_analysis_scores.pngIMG/bras_analysis_features.pngIMG/bras_analysis_correlation.pngIMG/bras_analysis_importance.pngMore detailed set (10k samples) in ds_analysis/:
ds_analysis/01_score_distributions.pngds_analysis/04_correlation_clustered.pngds_analysis/08_feature_importance.pngds_analysis/05_hexbin_relationships.pngRelated reports: docs/ras_whitepaper.md, docs/ras_verification_and_performance.md.
We want smooth, symmetric, and threshold-sensitive behavior for doubling. Since g(D)=tanh(D/σ) is a single function, this is naturally achieved.
Short findings (ds_analysis_doubling2/dataset.csv):
[-0.5,0.0]→~45.8, [0.0,0.5]→~54.1, [1.0,1.5]→~69.2, [2.0,2.5]→~81.0S_op = 100 − S_meKey visuals (doubling focus):
ds_analysis_doubling2/01_score_distributions.pngds_analysis_doubling2/07_statistical_tests.pngds_analysis_doubling2/08_feature_importance.pngpython test_bras.pypython analyze_bras.py.pypython data_science_analysis.py --n-samples 8000 --output-dir ds_analysis_doubling2Quick mathematical check (antisymmetry & transform):
python -c "import pandas as pd, numpy as np; df=pd.read_csv('ds_analysis_doubling2/dataset.csv'); \
print(np.abs(df['S_me']+df['S_op']-100).max()); \
print(np.abs((df['S_me']-50)/50 - np.tanh(df['D']/3)).max())"
With an antisymmetric, interpretable, and closed-form evaluation function, we have a fast, robust, and practical foundation for Backgammon. This provides a strong “pre-evaluator” for search/simulation and, on its own, makes a practical heuristic for mobile/edge deployment. The cube decisions benefit from smooth, symmetric thresholds. With new data, the weights can be fine-tuned and confidently recalibrated with the same analysis/test suite.
—
Sources and Code:
docs/ras_mathematical_foundations.mddocs/ras_whitepaper.mddocs/ras_verification_and_performance.mdbras_evaluator.pytest_bras.pyanalyze_bras.py.py, data_science_analysis.pyThis section is the longer version, where I answer "why, how, when" in detail, explaining design decisions and the validation process. Can be read like a blog series; skip between sections as needed.
Backgammon, while laden with dice uncertainty, still has regular position patterns: pip balance, bar disadvantage, home board power, prime and anchor architecture, blot risk, midboard control, etc. Two industry strategies dominate:
My aim is to combine the best of both: Single-pass, explainable, mathematically robust; mobile/edge speed, reportable consistency, calibratable with new data.
S ∈ [0,100]; easy for human-centric interpretation (percentile intuition)f_i should represent real game intuition, be normalizedHere each feature's game logic and normalization rationale are presented. Full definitions and denominators in docs/ras_mathematical_foundations.md.
f_pip): Total pip count difference; denominator 375 assures within bounds. See bras_evaluator.py:116.f_bar): Difference in checkers on the bar. Very penalizing since it kills short-term freedom. Code: bras_evaluator.py:179.f_off): Bear-off progress, endgame fuel. Code: bras_evaluator.py:187.f_hb): Closed points (1–6); proxy for jailing strength post-hit. Code: bras_evaluator.py:132.f_prime): Longest closed run (max 6); restricts movement. Code: bras_evaluator.py:149 + helper _longest_run at bras_evaluator.py:157.f_anch): Secure points in opponent's home, reduces getting closed out/gammoned. Code: bras_evaluator.py:170.f_blot): Open checker penalties, regionally weighted by ρ(i); home>mid>opp.home (1.5 / 1.0 / 1.2). Code: bras_evaluator.py:196, 100.f_stack): >5 checker stack penalty (flexibility loss). Code: bras_evaluator.py:206.f_out): Control over midboard (7–18 corridor). Code: bras_evaluator.py:195.f_x1): Home power × opponent's bar; strong home punishes opponent on bar more. Code: bras_evaluator.py:221.f_x2): Prime × opponent's anchor, counters primes somewhat, negative weight. Code: bras_evaluator.py:233.Normalization (denominators) serves: (1) Features can be summed on same scale; (2) Weight reflects direct impact on the score.
Initial weights are expert-driven, then pass a “checklist” data pass:
w_bar = 2.0w_pip = 2.2w_off = 1.6w_hb = 1.5, w_prime = 1.3w_blot = 1.1w_out = 0.5w_anch = 0.6w_stack = 0.4w_x1 = 1.0, w_x2 = -0.6After data, ranking by |w|·std; practically, pip, bar, off, blot dominate (see plots and tables).
tanh is naturally odd, i.e., g(-x)=-g(x), making it ideal for antisymmetric design. Bounded to [-1,1], smooth in center, well-behaved derivative. σ=3 calibration achieves:
D in [-3,3], so score band is ~50±38; extremes separated but not oversaturatedLogistic also considered, but tanh + affine map (50±50·g) is cleaner for centering and symmetry.
Flip operator: Ŷ_i := O_{25−i}, Ô_i := Y_{25−i}, b_Y↔b_O, y_Y↔y_O. This flips all feature signs → f_i(tilde) = −f_i. Hence D(tilde) = −D, S_me(tilde) = 100 − S_me. In implementation: bras_evaluator.py:306.
From the doc, for pip:
∂S_me/∂R = 50·g’(D)·w_pip/375 = 50·w_pip/(375·σ)·sech²(D/σ) > 0
Bar increase for me is bad → ∂S_me/∂b_Y < 0. This is scenario tested in test_bras.py:303.
Key code choices:
~0.78 ms/position. See: generation loop in analyze_bras.py.py._longest_run computes prime length via linear scan with early break and small buffer.rho(i) and rho_star(i) encode location-dependent blot risk (home, mid, opp.home), integrating “point risk isn’t uniform” into the game.Tests in test_bras.py cover five axes:
1e−14. (test_bras.py:139)50.000, contact ex: S≈47.893, D≈−0.1265. (test_bras.py:192)f_i ∈ [-1,1] checked, no violations. (test_bras.py:240)S ∈ [0,100] checked, no violations. (test_bras.py:274)test_bras.py:303)test_bras.py:402)Random generator focuses on certain points (to increase stack frequency), see: test_bras.py:467.
Two layers of reports:
analyze_bras.py.py): summarizing score, D, transform, and antisymmetrydata_science_analysis.py): EDA, correlation, importance, VIF, dimensionality reduction, clustering, sensitivitySample visuals (general):
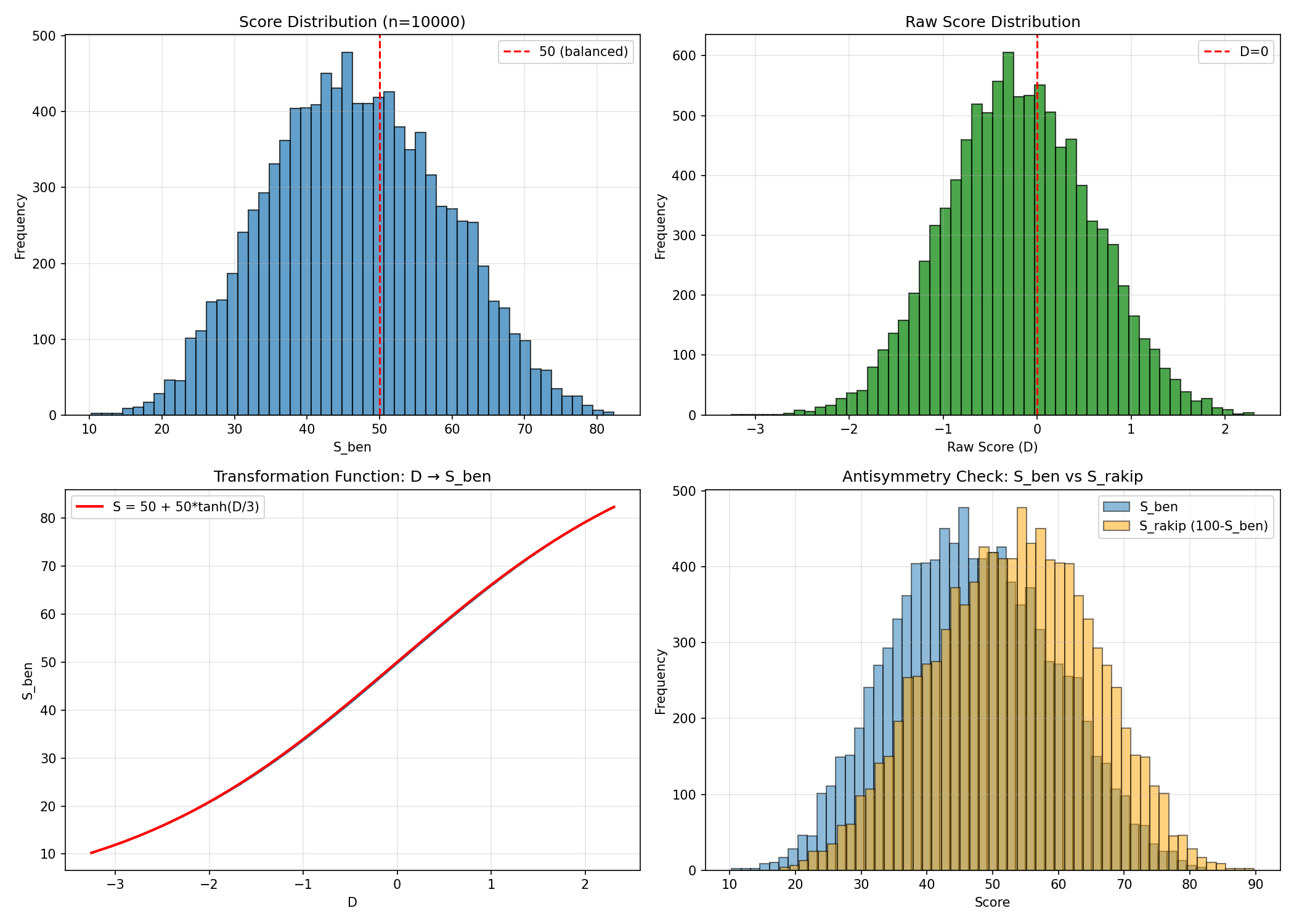
bras_analysis_scores.png
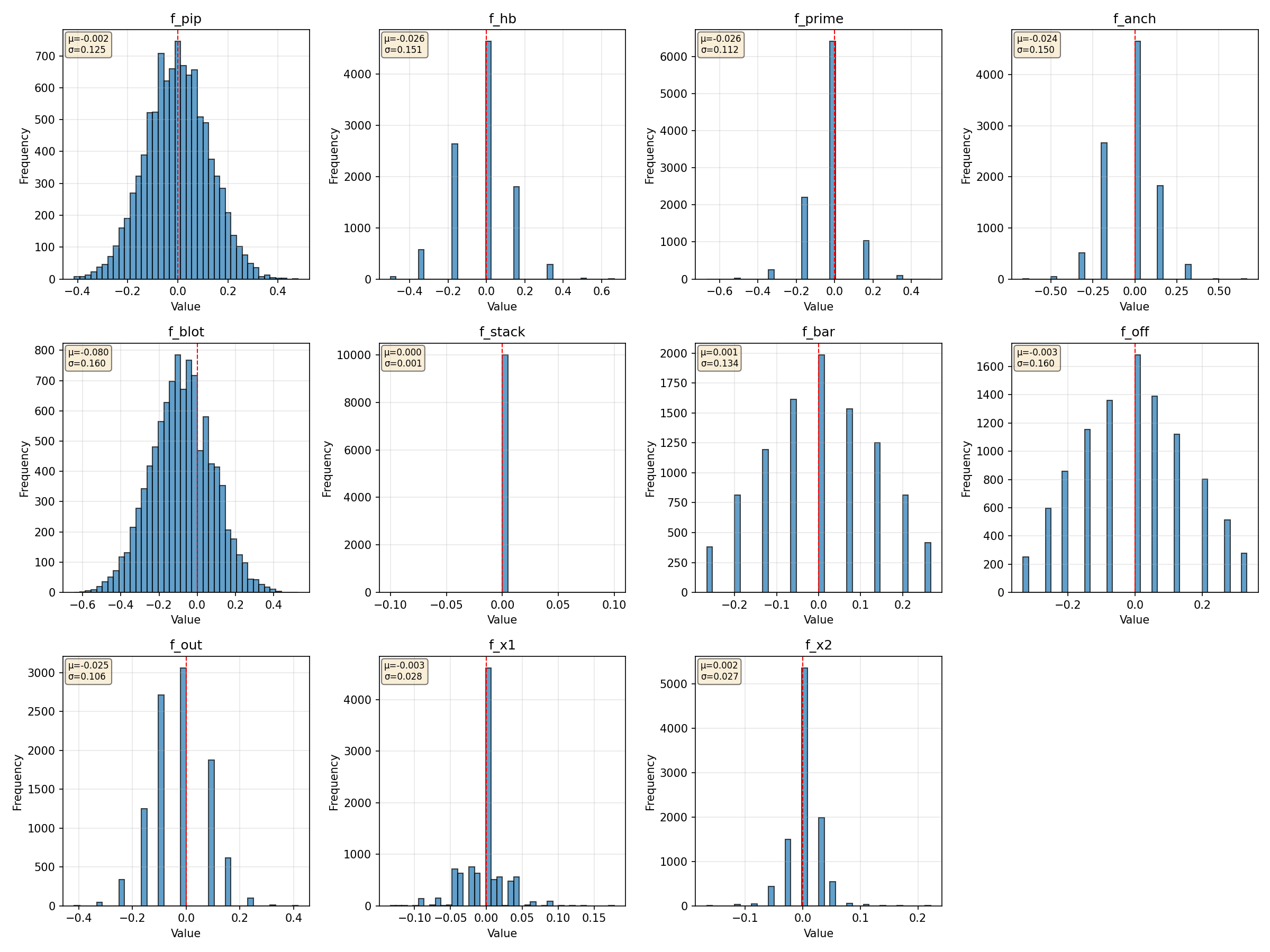
bras_analysis_features.png
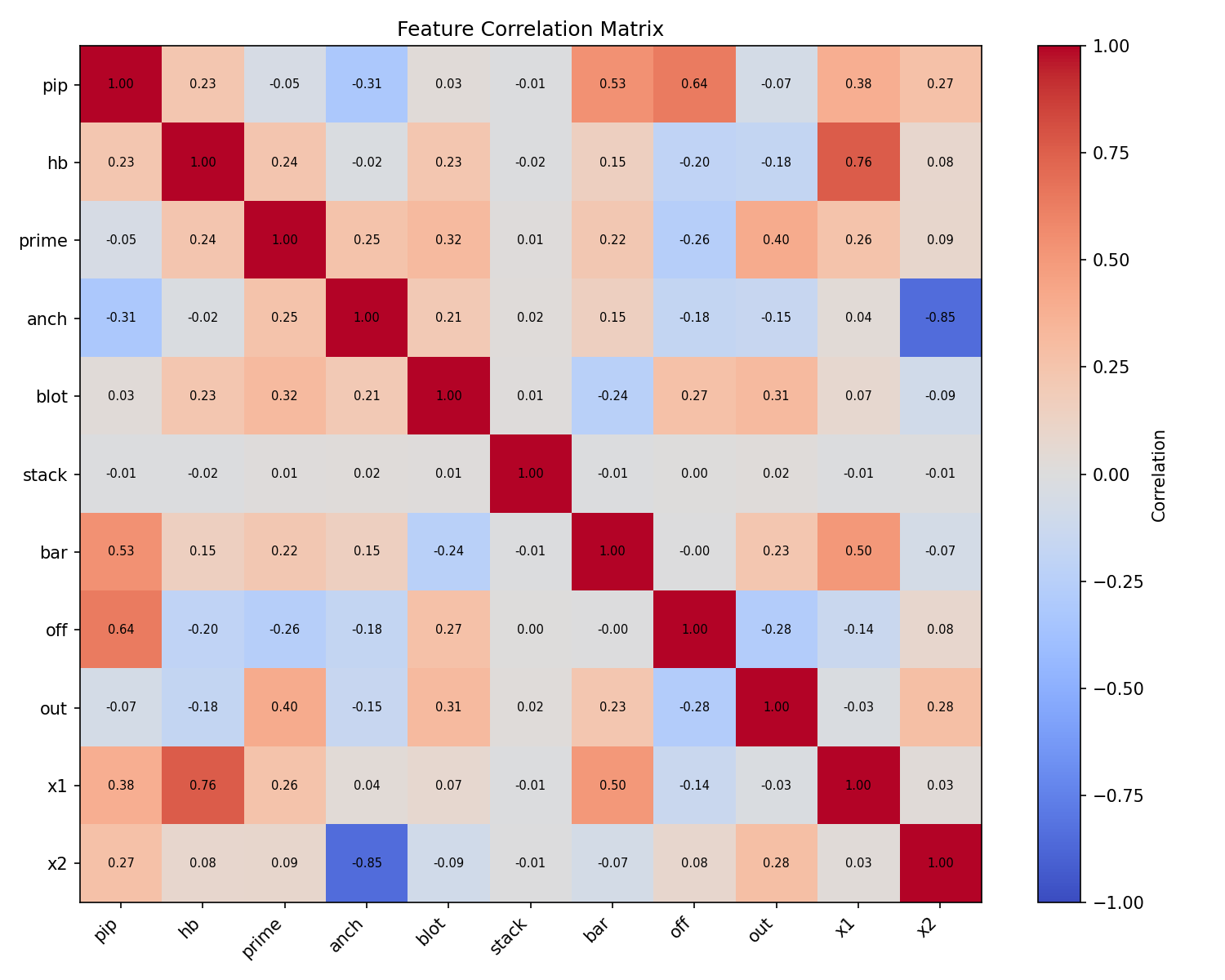
bras_analysis_correlation.png
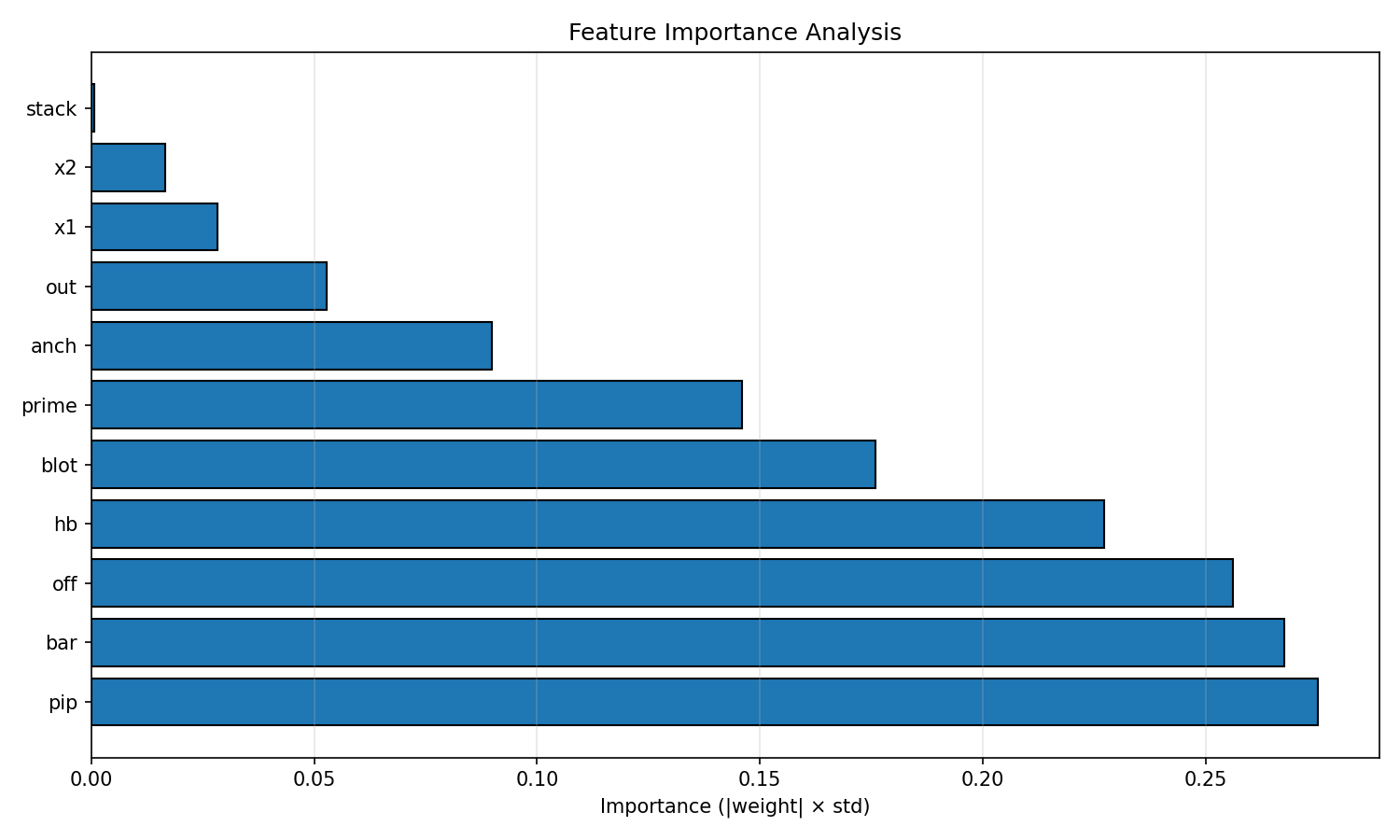
bras_analysis_importance.png
Detailed set (10k samples, ds_analysis/):
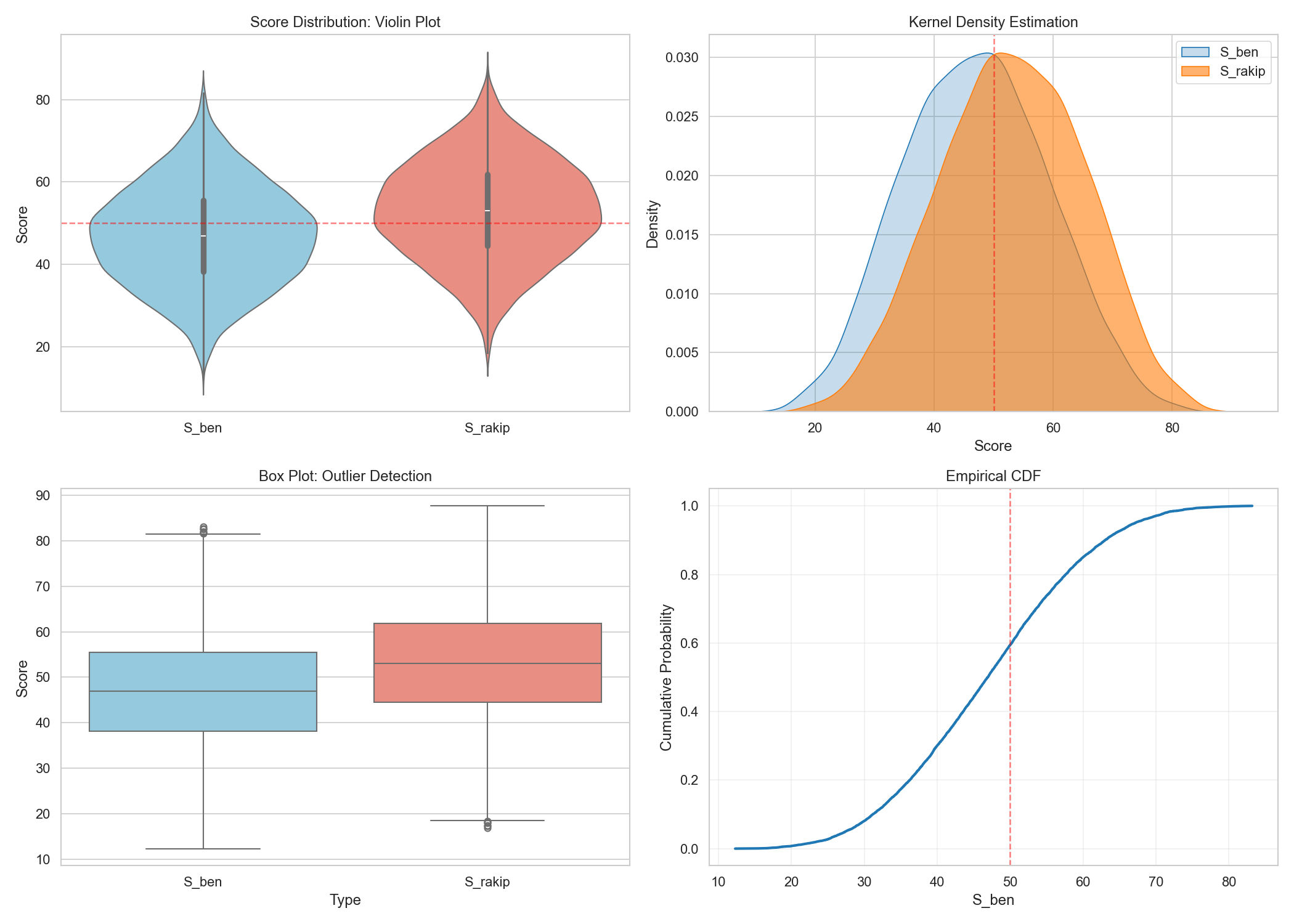
01_score_distributions.png
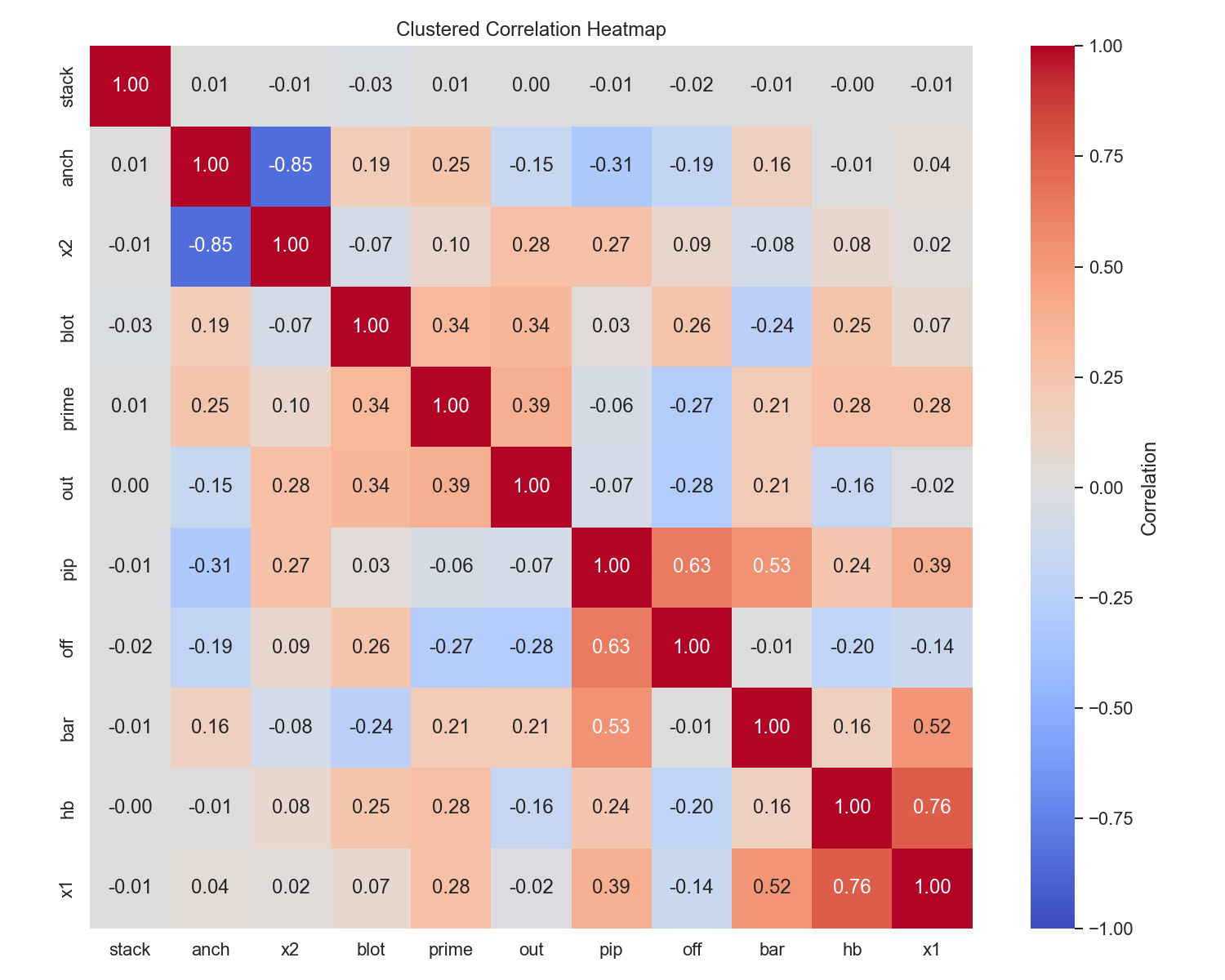
04_correlation_clustered.png
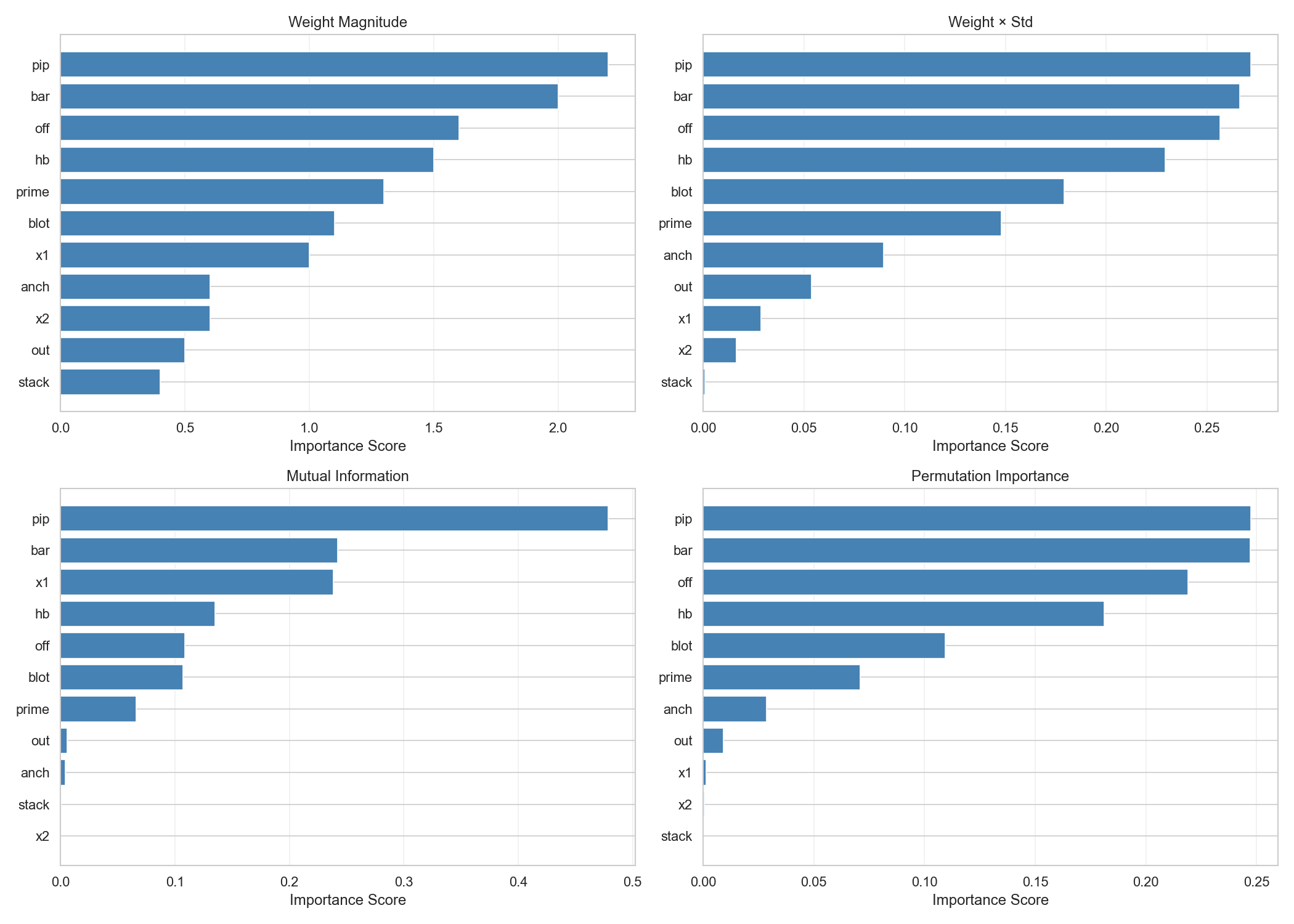
08_feature_importance.png
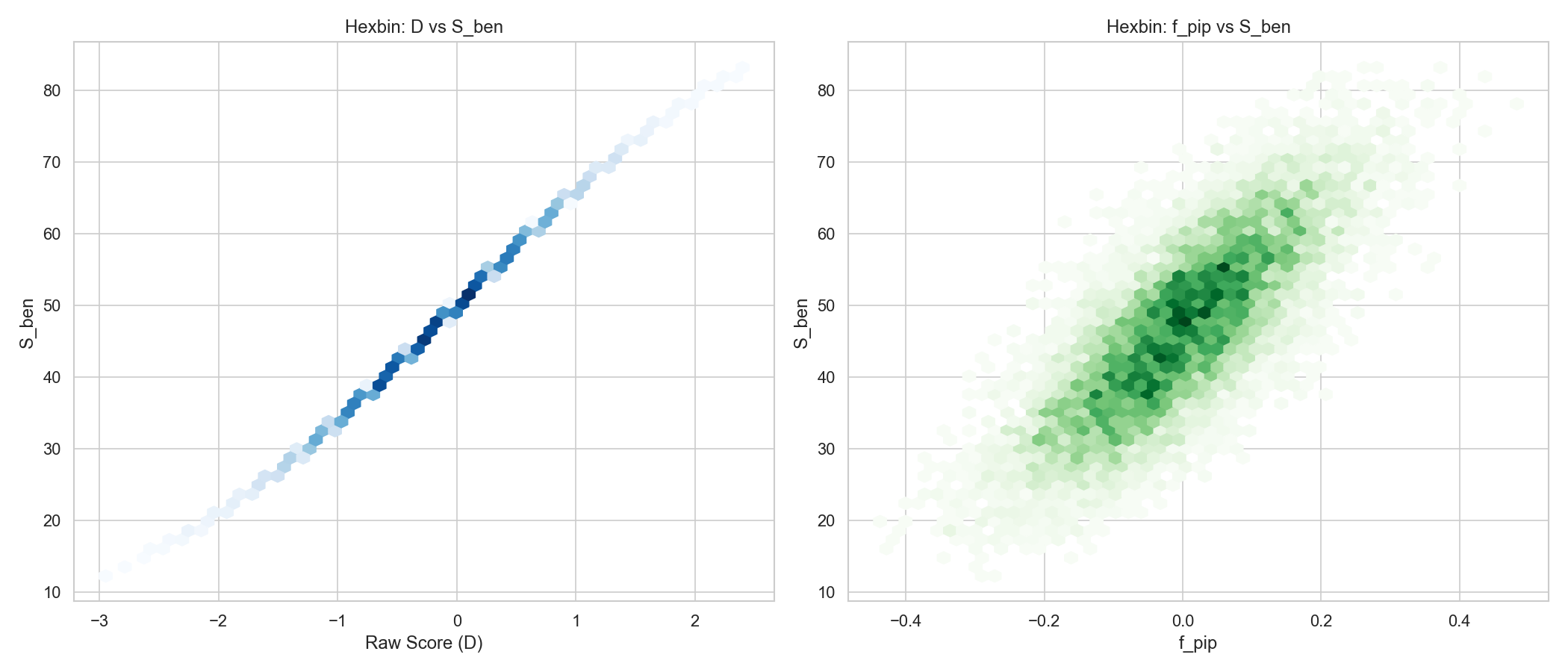
05_hexbin_relationships.png
Doubling is thresholded by nature; g(D)=tanh(D/σ) makes this transition smooth. From ds_analysis_doubling2/dataset.csv:
E[p]≈0.500, std≈0.145.[-0.5,0.0]→S≈45.8, [0.0,0.5]→S≈54.1, [1.0,1.5]→S≈69.2, [2.0,2.5]→S≈81.0.S_op=100−S_me.This cleanly splits “initial double” and “drop” regions. Surface is also uniform, does not jump with small noise.
Doubling visuals (samples):
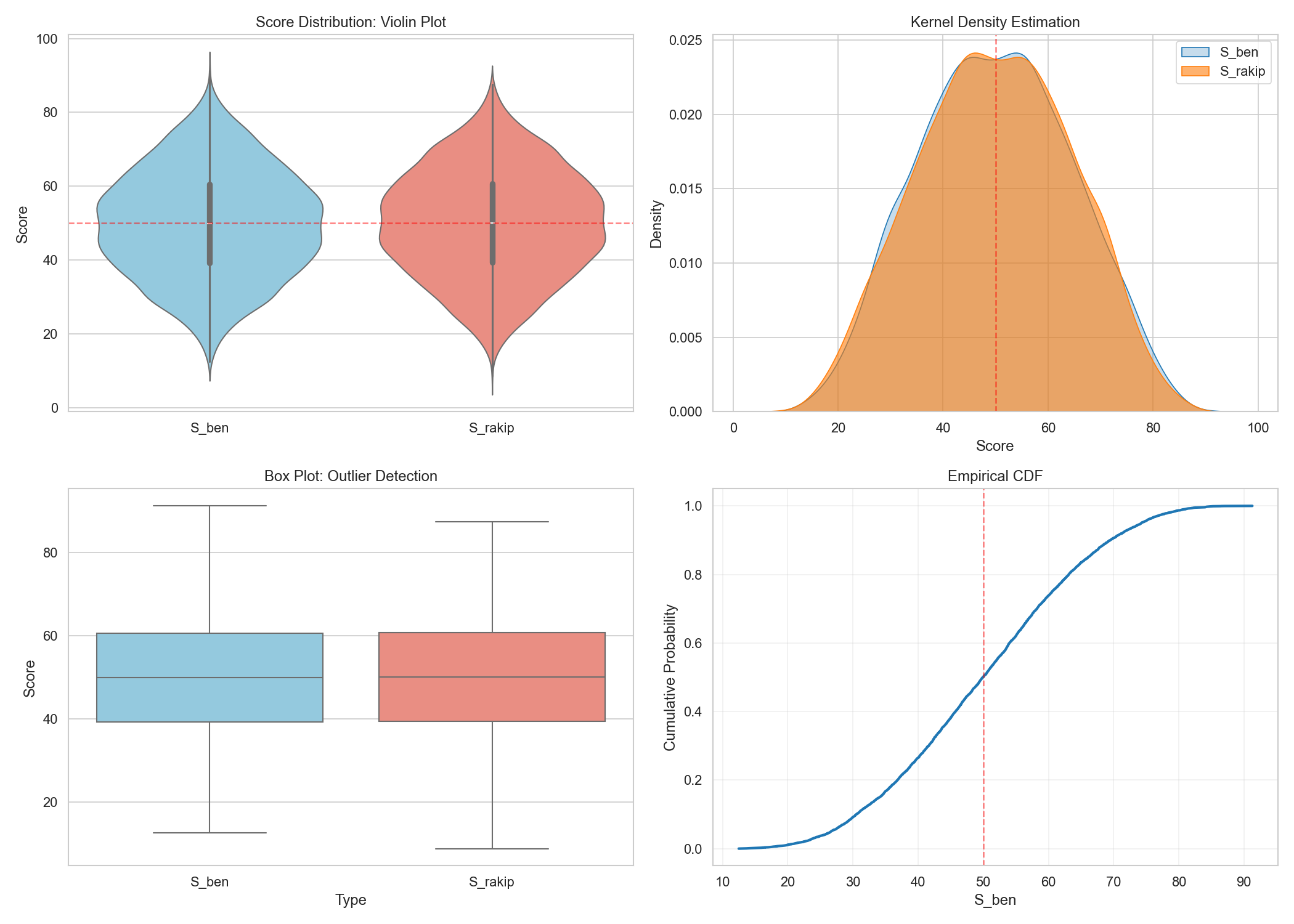
01_score_distributions.png
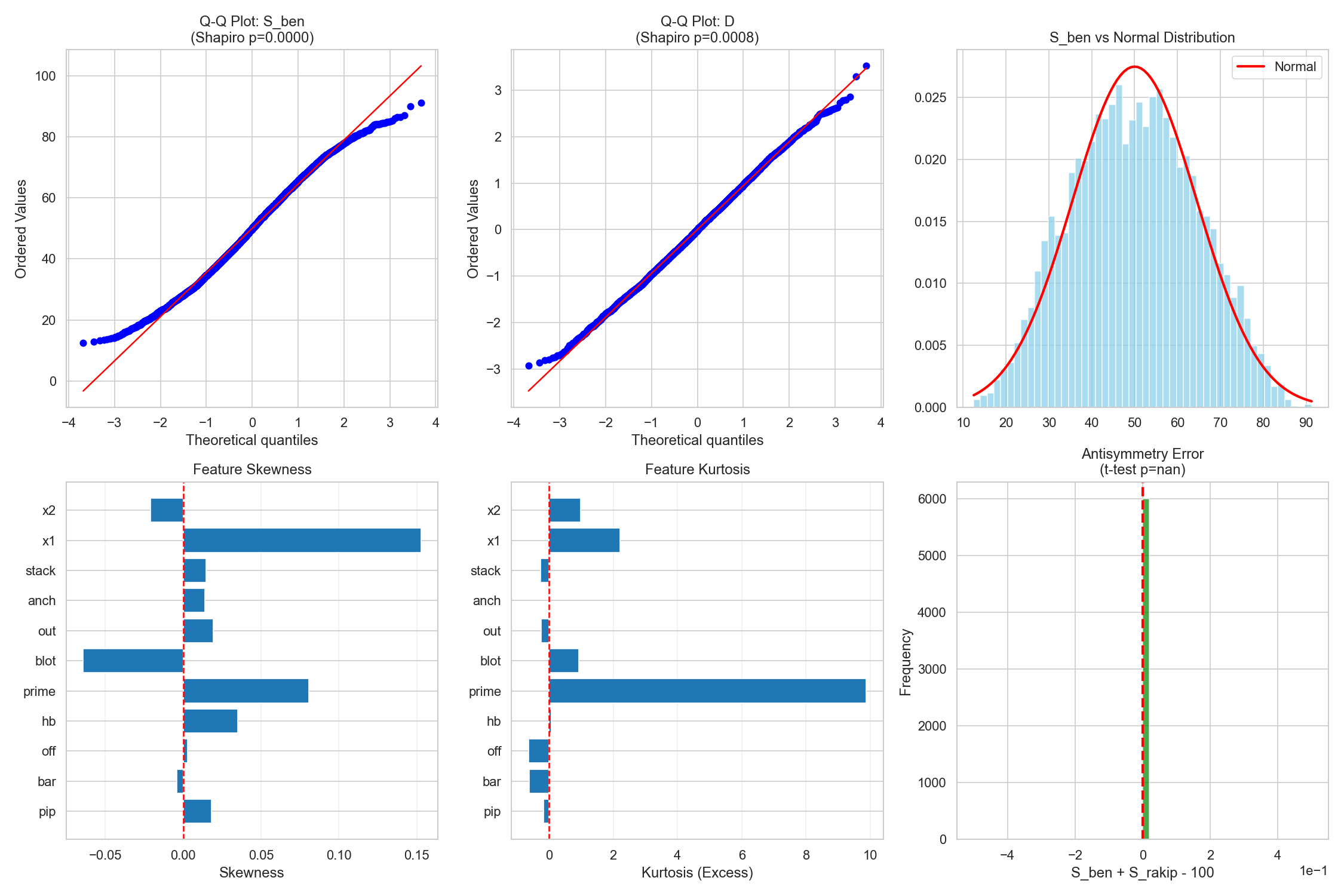
07_statistical_tests.png
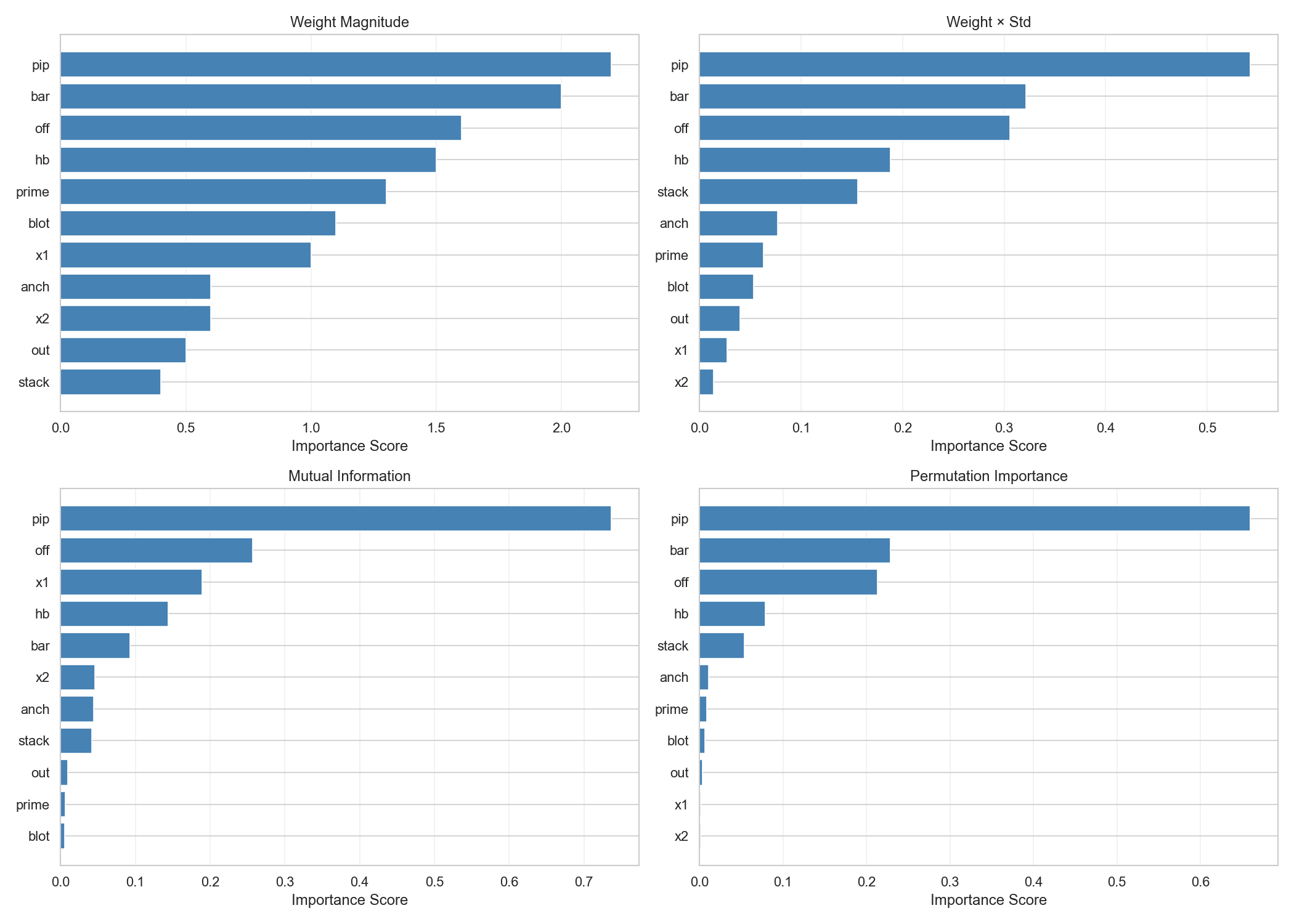
08_feature_importance.png
w and σ.Basic tests:
python test_bras.py
Quick analysis and visuals:
python analyze_bras.py.py
Data science pipeline (with parameters):
python data_science_analysis.py --n-samples 8000 --output-dir ds_analysis_doubling2
Quick math validation:
python -c "import pandas as pd, numpy as np; df=pd.read_csv('ds_analysis_doubling2/dataset.csv'); \
print(np.abs(df['S_me']+df['S_op']-100).max()); \
print(np.abs((df['S_me']-50)/50 - np.tanh(df['D']/3)).max())"
import numpy as np
from tavla_evaluator import TavlaEvaluator, create_opening_position
e = TavlaEvaluator()
pos = create_opening_position()
S_me, S_op = e.compute_score(pos)
print(S_me, S_op)
# Detailed output
detail = e.evaluate_detailed(pos)
print(detail['features'])
print(detail['D'], detail['g'])
A good evaluation function isn’t so much “correct” as it is “consistent and useful.” This approach balances speed/fidelity/interpretability for Backgammon. It smooths the cube decision surface, gives a robust prior for search/simulation, and serves as a practical heuristic by itself for mobile/edge. Very receptive to improvement with feedback and new data.